[Deep learning] 신경망 기초5; Regularization Strategies(학습규제전략) - 일반적방지(Early Stopping, Weight Decay, Dropout, Weight Constraint,) & Learning Rate 조절 방식

Neural Networks는 매개변수가 아주 많은 모델이어서 훈련 데이터에 쉽게 Overfitting문제 발생. 이 문제를 해결하는 가장 중요한 방법은 가중치 규제 전략이다.

 

일반적인 overfitting을 방지 방식

1. Early Stopping
   : 뇌절하지 않도록 적절한 선에서 epoch를 중지시켜 학습을 끊어주는것.
   
   
2. Weight Decay (가중치 감소)
   : 손실함수에 가중치의 합을 더해주어서 가중치가 너무 크게 업데이트 되는 것을 방지한다.
   loss함수에 λ값을 곱한 가중치 합을 더해서 진행. 
   L(θw)=12Σi(outputi−targeti)2+λ|θw|
   ( L1:절대값을 사용해서 ;0에수렴)
   L(θw)=12Σi(outputi−targeti)2+λ||θw||2
   (L2:제곱값을 사용해서 ;0에가까이가지만0에는수렴하지 않는다)
   

   

   # Weight Decay를 전체적으로 반영한 예시 코드
   from tensorflow.keras.constraints import MaxNorm
   from tensorflow.keras import regularizers
   
   # 모델 구성을 확인합니다.
   model = Sequential([
       Flatten(input_shape=(28, 28)),
       Dense(64, 
               kernel_regularizer=regularizers.l2(0.01),    # L2 norm regularization
               activity_regularizer=regularizers.l1(0.01)), # L1 norm regularization    
       Dense(10, activation='softmax')
   ])
   # 업데이트 방식을 설정합니다.
   model.compile(optimizer='adam'
                , loss='sparse_categorical_crossentropy'
                , metrics=['accuracy'])
   model.summary()
   
   model.fit(X_train, y_train, batch_size=30, epochs=1, verbose=1, 
             validation_data=(X_test,y_test))​

3. Dropout
   : 학습할때만 랜덤으로 노드수를 꺼서 활성화된 노드들의 성능을 향상시키는 방식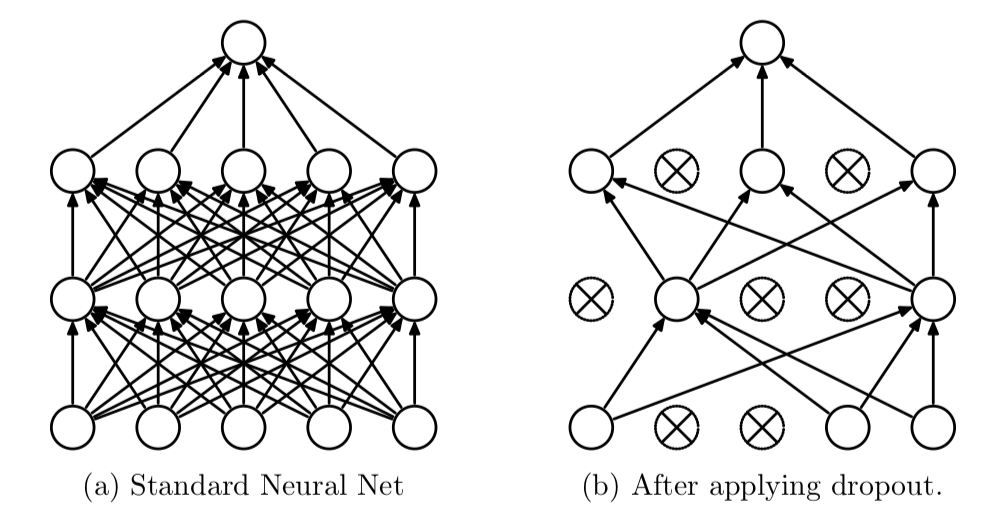
   

   

   # Dropout을 적용시킨 모델
   from tensorflow.keras.layers import Dropout
   from tensorflow.keras.constraints import MaxNorm
   from tensorflow.keras import regularizers
   # 모델 구성을 확인합니다.
   model = Sequential([
       Flatten(input_shape=(28, 28)),
       Dense(64, 
               kernel_regularizer=regularizers.l2(0.01),
               activity_regularizer=regularizers.l1(0.01),
               kernel_constraint=MaxNorm(2.)),             
       Dropout(0.5)       ,                                   ## add dropout
       Dense(10, activation='softmax')
   ])
   # 업데이트 방식을 설정합니다.
   model.compile(optimizer='adam'
                , loss='sparse_categorical_crossentropy'
                , metrics=['accuracy'])
   model.summary()
   
   
   model.fit(X_train, y_train, batch_size=30, epochs=1, verbose=1, 
             validation_data=(X_test,y_test))​

4. Weight Constraint
   : 가중치가 가질수 있는 값의 범위를 정하고 그 정한값을 넘어가면 정한값이 출력되게하는 물리적인 가중치 억제 방식
   

   # Weight constraints 적용 kernel_constraint=MaxNorm(2.) 모델 구성을 확인합니다.
   model = Sequential([
       Flatten(input_shape=(28, 28)),
       Dense(64, 
               kernel_regularizer=regularizers.l2(0.01),
               activity_regularizer=regularizers.l1(0.01),
               kernel_constraint=MaxNorm(2.)),             ## add constraints
       Dense(10, activation='softmax')
   ])
   # 업데이트 방식을 설정합니다.
   model.compile(optimizer='adam'
                , loss='sparse_categorical_crossentropy'
                , metrics=['accuracy'])
   model.summary()
   
   
   model.fit(X_train, y_train, batch_size=30, epochs=1, verbose=1, 
             validation_data=(X_test,y_test))​

Learning Late 조절을 통한 Overfitting 방지 방식

알고리즘의 목적함수를 optimizing 할 때, 경사하강법(gradient descent) 기반의 최적화 알고리즘을 적용하는 경우,
학습률 η를 결정함에 있어 고정된 하나의 값으로 학습률을 사용하지 않고 학습 반복이 진행됨에 따라 미리 정해놓은 스케쥴대로 학습률을 변경하는(늘리거나 줄이는) 전략을 Learning (Rate) Schedule 이라고 한다.

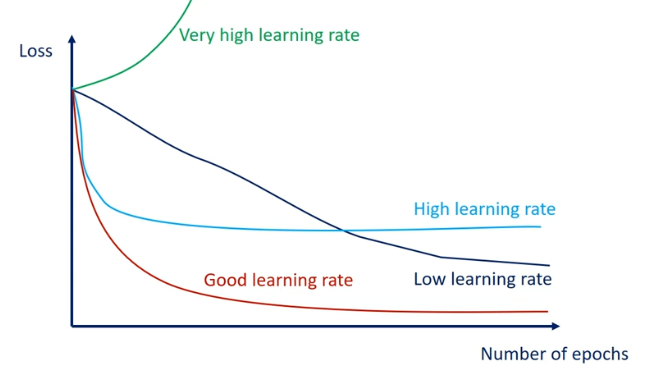
고정된 학습률을 사용할 경우

• 학습률 η가 작다면 수렴속도가 느리며, local minimum에 수렴되어 최선이 아닌 solution을 얻게될 수 있다.
• 학습률 η가 크다면 local minimum은 쉽게 탈출할 수 있겠지만 최적점 근처에서 진동이 심해 수렴하지 못하거나, 극단적인 경우 알고리즘이 발산해버릴 수 있다 이런 경우 local minimum은 피하면서 global minimum에는 수렴하는 적절한 고정 학습률을 찾아낸다면 좋겠지만 이것은 어려운 문제이며 보다 더 효율적인 방법이 있다.

1. Learning rate decay

model.compile(optimizer=tf.keras.optimizers.Adam(lr=0.001, beta_1 = 0.89)
             , loss='sparse_categorical_crossentropy'
             , metrics=['accuracy'])
model.summary()


model.fit(X_train, y_train, batch_size=30, epochs=1, verbose=1, 
          validation_data=(X_test,y_test))

2. Learning Rate Scheduling

lr_schedule = keras.optimizers.schedules.ExponentialDecay(
    initial_learning_rate=1e-2,
    decay_steps=10000,
    decay_rate=0.9)

model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=lr_schedule)
             , loss='sparse_categorical_crossentropy'
             , metrics=['accuracy'])
model.summary()


model.fit(X_train, y_train, batch_size=30, epochs=1, verbose=1, 
          validation_data=(X_test,y_test))

3. decayed learning rate

def decayed_learning_rate(step):
  step = min(step, decay_steps)
  cosine_decay = 0.5 * (1 + cos(pi * step / decay_steps))
  decayed = (1 - alpha) * cosine_decay + alpha
  return initial_learning_rate * decayed

first_decay_steps = 1000
initial_learning_rate = 0.01
lr_decayed_fn = (
  tf.keras.experimental.CosineDecayRestarts(
      initial_learning_rate,
      first_decay_steps))

model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=lr_schedule)
             , loss='sparse_categorical_crossentropy'
             , metrics=['accuracy'])
model.summary()


model.fit(X_train, y_train, batch_size=30, epochs=1, verbose=1, 
          validation_data=(X_test,y_test))

 

• iterration = 데이터수/배치 사이즈
• 배치batch = 1번 학습할 때의 사용할 데이트의 개수 -->배치사이즈가 크면 메모리를 많이 잡아먹는다(병렬처리방식) /배치사이즈가 작으면 학습 시간이 오래걸린다. 
  생성되는 배치의 개수는 전체 데이터셋의 수 / batch_size 를 계산한 뒤 올림한 자연수 값으로 결정.
• 이포크epoch = 전체 데이터가 학습되는 횟수. 
  
  • 이포크가 크면 -> 과적합, 학습이 오래걸림. (해결: 얼리 스타핑)
  • 이포크가 작으면 -> 과소적합, 학습이 제대로 이루어지지 않는다. 

 

ref. https://velog.io/@changdaeoh/learningrateschedule

[학습률 스케쥴링] Cyclical Learning Rate Schedule - Cosine Decay Restarts / Cosine Annealing