리스트나 스택 또는 큐로 가계도나 조직도를 구현할 수 있을까요?
선형 자료구조로 계층형 구조를 표현하기 어렵습니다.
이처럼 가계도와 같은 계층형 구조를 가진 문제를 해결하기 위한 자료구조 형태가 트리입니다.
트리 관련 용어
- 루트 노드(Root node)
부모가 없는 최상위 노드 - 단말 노드 (leaf node)
자식이 없는 최말단 노드 - 형제 노드 (sibling node)
부모가 같은 두 개의 노드 - 서브 트리 (sub tree)
자식노드이면서 부모노드역할을 하는 노드가 있는 트리 - 레벨 (level)
루트노드에서 얼마나 멀리 떨어져 있는지 각각 나타낸다. 루트노드의 레벨은 0이며, 아래로 내려갈때마다 1씩증가한다 - 크기(size)
트리에 포함된 모든 노드의 개수 - 깊이 (depth)
루트 노드부터의 거리 - 높이(height)
깊이 중 최댓값, 리프 레벨의 최대값 - 차수(degree)
각 노드의 (자식 방향)간선 개수
기본적으로 트리의 크기가 n 일때 전체 간선의 개수는 n-1

트리의 종류
- 이진 트리 :
순회는 재귀 호출을 사용한다. 따라서 전위, 중위, 후위 순회를 간단하게 구현 할 수 있다. - 스레드 이진 트리 :
재귀 호출 없이 순회 할 수 있도록 구현된 트리. 이진 트리의 단점(외부스택 관리필요, 하위레벨로 갈수록 재귀 호출의 depth 깊어져 비효율 발생가능) 보완. - 이진 탐색 트리 Binary Search Trees(BST) :
이진트리보다 빠른 노드 탐색이 목적. 따라서 트리를 효율적으로 구현하고 사용하기 위해서 일정한 조건으로 정의. 탐색용 자료구조로 사용되어 노드의 크기에 따라 위치를 정의한다.- BST의 목적은 단순 이진트리보다 빠른 노드탐색이다. 때문에 insert node에서 중복을 처리해주는 것이 아닌, 아래 '값 크기 조건'에 맞도록 값을 넣어주는 경우
- 특징: 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드
부모노드보다 왼쪽 자식 노드가 작고 오른쪽 자식 노드는 크다. - 왼쪽 -> 오른쪽 순서 개념이 적용되는 이유 : 트리와 같은 자료구조는 기본이 되는 연결리스트를 참조해서 만들어진 개념이기 때문이다.
- 중복값을 가지고 있는 노드가 없다.
- AVL 트리 :
- 이진 탐색 트리는 좌우 균형이 잘 맞으면 탐생 성능이 높다. 각 노드의 왼쪽 서브 트리의 높이와 오른쪽 서브 트리의 높이를 비교하여 트리의 균형을 조절.
- (+)히프 :
- 노드중에서 키값이 가장 큰 노드나 가장 작은 노드를 찾기 위해 만든 자료구조다.
이진트리
'''이진트리의 자료구조 소스코드'''
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def __str__(self):
return str(self.data)
class Tree:
def __init__(self):
self.root = None
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
'''tree 초기화'''
root = Node(10)
root.left = Node(34)
root.right = Node(89)
root.left.left = Node(45)
root.left.right = Node(50)
# '''python 라이브러리 사용해서 트리만들기 pip install anytree'''
# from anytree import Node, RenderTree
# root = Node(10)
# level_1_child_1 = Node(34, parent=root)
# level_1_child_2 = Node(89, parent=root)
# level_2_child_1 = Node(45, parent=level_1_child_1)
# level_2_child_2 = Node(50, parent=level_1_child_1)
# level_2_child_3 = Node(15, parent=level_1_child_2)
# for pre, fill, node in RenderTree(root):
# print("%s%s" % (pre, node.name))
# # Tree Structure
# # 10 --- root
# # / \
# # 34 89 --- Level 1
# # / \ /
# # 45 50 15 --- Level 2
'''
10
├── 34
│ ├── 45
│ └── 50
└── 89
└── 15
'''
def preorder(node):
if node:
print(node.data)
preorder(node.left)
preorder(node.right)
def inorder(node):
if node:
inorder(node.left)
print(node.data)
inorder(node.right)
def postorder(node):
if node:
postorder(node.left)
postorder(node.right)
print(node.data)
순회 (Traversal)
그래프 또는 트리처럼 연결된 구조에서 노드를 한 번씩 탐색하는 개념
그래프와 트리의 순회구분
- 그래프의 순회는 DFS(깊이우선탐색), BFS(너비우선탐색) 방법이 있다.
- DFS, BFS는 탐색 알고리즘이다.
- 트리의 순회는 전위, 중위, 후위순회이다.
트리의 순회 (Tree Traversal)
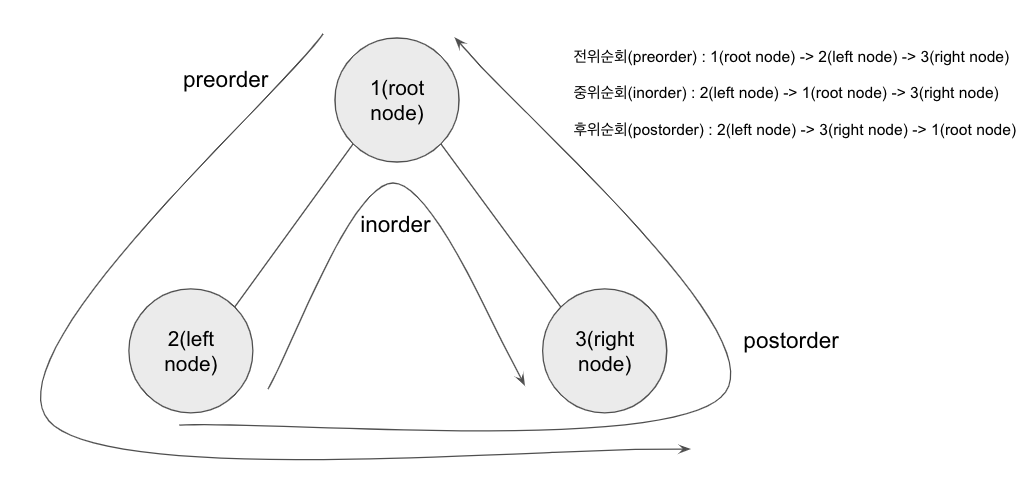
- 전위 순회 (Pre-order Traversal)
- 해당 노드를 출력하고 왼쪽으로 이동, 왼쪽 노드가 존재하면 계속해서 왼쩍으로 이동 하여 출력 하고 왼쪽이 끝나는 노드부터 오른쪽 노드를 순회.
- 전위 순회는 DLR 순서로 순회한다.
- D : 현재 노드(루트 노드)를 먼저 방문한다
- L : 현재 노드 왼쪽 서브트리로 이동한다
- R : 현재 노드 오른쪽 서브트리로 이동한다
-
def preorderTraversal(self, node): print(node, end='') if not node.left == None : self.preorderTraversal(node.left) if not node.right == None : self.preorderTraversal(node.right)
- 중위 순회 (In-order Traversal)
- 중위 순회는 LDR순으로 순회. 왼쪽 순회가 우선이고 출력이 중앙에 위치
-
def inorderTraversal(self, node): if not node.left == None : self.inorderTraversal(node.left) print(node, end='') if not node.right == None : self.inorderTraversal(node.right)
- 후위 순회 (Post-order Traversal)
- 후위 순회 LRD순으로 순회. 출력이 마지막에 위치.
-
def postorderTraversal(self, node): if not node.left == None : self.postorderTraversal(node.left) if not node.right == None : self.postorderTraversal(node.right) print(node, end='')
'''이진트리의 순회 코드 + 트리구조 코드'''
#노드 클래스 지정
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def __str__(self):
return str(self.data)
#트리 클래스 지정
class Tree:
def __init__(self):
self.root = None
# 전위 순회
def preorderTraversal(self, node):
print(node, end='') # 현재 노드 출력
if not node.left == None :
self.preorderTraversal(node.left) # 왼쪽 노드가 비어있지 않으면 왼쪽 노드 추가 재귀함수
if not node.right == None :
self.preorderTraversal(node.right) # 오른쪽 노드가 비어있지 않으면 오른쪽 노드 추가 재귀함수
# 중위 순회
def inorderTraversal(self, node):
if not node.left == None :
self.inorderTraversal(node.left) # 왼쪽 노드가 비어있지 않으면 왼쪽 노드 추가 재귀함수
print(node, end='') # 현재 노드 출력
if not node.right == None :
self.inorderTraversal(node.right) # 오른쪽 노드가 비어있지 않으면 오른쪽 노드 추가 재귀함수
# 후위 순회
def postorderTraversal(self, node):
if not node.left == None :
self.postorderTraversal(node.left) # 왼쪽 노드가 비어있지 않으면 왼쪽 노드 추가 재귀함수
if not node.right == None :
self.postorderTraversal(node.right) # 오른쪽 노드가 비어있지 않으면 오른쪽 노드 추가 재귀함수
print(node, end='') # 현재 노드 출력
# root 노드 만드는 함수
def makeRoot(self, node, left_node, right_node):
if self.root == None: # root 초기화
self.root = node # root = 노드
node.left = left_node #
node.right = right_node
if __name__ == "__main__":
node = []
node.append(Node('-'))
node.append(Node('*'))
node.append(Node('/'))
node.append(Node('A'))
node.append(Node('B'))
node.append(Node('C'))
node.append(Node('D'))
m_tree = Tree()
for i in range(int(len(node)/2)): # for i in 3 --> i = 0, 1, 2
m_tree.makeRoot(node[i],node[i*2+1],node[i*2+2])
print( '전위 순회 : ', end='') ; m_tree.preorderTraversal(m_tree.root)
print('\n' + '중위 순회 : ', end='') ; m_tree.inorderTraversal(m_tree.root)
print('\n' + '후위 순회 : ', end='') ; m_tree.postorderTraversal(m_tree.root)
이진 탐색 트리
- 모든 원소는 서로 다른 키를 갖는다.
- 왼쪽 서브 트리에 있는 원소들은 루트의 키보다 작다.
- 오른쪽 서브 트리에 있는 원소들은 루트의 키보다 크다.
- 왼쪽 서브 트리와 오른쪽 서브 트리도 이진 탐색 트리이다.
'''원소 삽입'''
def insertElement(self, data):
new_node = Node(data)
if self.root == None:
self.root = new_node
node = self.root
while True:
pre_node = node
# 새 노드의 데이터가 작으면
# 왼쪽으로 이동
if node.data > new_node.data:
node = node.left
# 이동한 노드가 빈 노드면 노드 추가
if node == None:
node = new_node
pre_node.left = node
# 새 노드의 데이터가 크면
# 오른쪽으로 이동
elif node.data < new_node.data:
node = node.right
if node == None:
node = new_node
pre_node.right = node
else: return # 똑같은 키가 있으면 취소
''' 원소 탐색 '''
def searchElement(self, data):
node = self.root
while True:
if node.data > data:
node = node.left
elif node.data < data:
node = node.right
elif node.data == data:
break
else:
return Node('탐색 결과 없음')
return node #삽입과 같으나 같은 값이 있으면 노드를 반환한다.import random
class Node:
def __init__(self, data):
self.data = data
self.right = None
self.left = None
def __str__(self):
return str(self.data)
class SearchTree:
def __init__(self):
self.root = None
def insertElement(self, data):
new_node = Node(data)
if self.root == None:
self.root = new_node
node = self.root
while True:
pre_node = node
if node.data > new_node.data:
node = node.left
if node == None:
node = new_node
pre_node.left = node
elif node.data < new_node.data:
node = node.right
if node == None:
node = new_node
pre_node.right = node
else: return
def searchElement(self, data):
node = self.root
while True:
if node.data > data:
node = node.left
elif node.data < data:
node = node.right
elif node.data == data:
break
else:
return Node('탐색 결과 없음')
return node
def preorderTraversal(self, node):
print(node, end=' ')
if not node.left == None : self.preorderTraversal(node.left)
if not node.right == None : self.preorderTraversal(node.right)
def inorderTraversal(self, node):
if not node.left == None : self.inorderTraversal(node.left)
print(node, end=' ')
if not node.right == None : self.inorderTraversal(node.right)
def postorderTraversal(self, node):
if not node.left == None : self.postorderTraversal(node.left)
if not node.right == None : self.postorderTraversal(node.right)
print(node, end=' ')
if __name__ == "__main__":
m_tree = SearchTree()
m_tree.insertElement(250)
for i in range(20):
m_tree.insertElement(random.randint(0,500))
print( '전위 순회 : ', end='') ; m_tree.preorderTraversal(m_tree.root)
print('\n' + '중위 순회 : ', end='') ; m_tree.inorderTraversal(m_tree.root)
print('\n' + '후위 순회 : ', end='') ; m_tree.postorderTraversal(m_tree.root)
node = m_tree.searchElement(250)
print('\n' + '탐색한 노드의 값 :', node)
print( '노드의 왼쪽 서브 트리 :', node.left)
print( '노드의 오른쪽 서브 트리 :', node.right)
node = m_tree.searchElement(node.left.data)
print('\n' + '탐색한 노드의 값 :', node)
print( '노드의 왼쪽 서브 트리 :', node.left)
print( '노드의 오른쪽 서브 트리 :', node.right)
'''
전위 순회 : 250 90 81 28 60 87 93 91 129 179 401 313 274 278 370 332 439 426 402 414 464
중위 순회 : 28 60 81 87 90 91 93 129 179 250 274 278 313 332 370 401 402 414 426 439 464
후위 순회 : 60 28 87 81 91 179 129 93 90 278 274 332 370 313 414 402 426 464 439 401 250
탐색한 노드의 값 : 250
노드의 왼쪽 서브 트리 : 90
노드의 오른쪽 서브 트리 : 401
탐색한 노드의 값 : 90
노드의 왼쪽 서브 트리 : 81
노드의 오른쪽 서브 트리 : 93
'''
스레드 이진 트리
서브 트리가 존재하지 않는 노드의 링크를 순회 경로에 따라 선행자 또는 후행자로 지정하여 재귀 호출을 사용하지 않고 순회 할 수 있다.
중위 순회
스레드 이진 트리의 중위 순회는 재귀 호출을 사용하지 않는다.
def inorderTraversal(self, node):
while not node.left == None:
node = node.left
print(node, end='')
ref.
파이썬으로 구현한 자료구조 - 트리 — baealex
트리(Tree) 리스트나 스택 또는 큐로 가계도나 조직도를 구현할 수 있을까요? 선형 자료구조로 계층형 구조를 표현하기 어렵습니다. 이처럼 계층형 구조를 가진 문제를 해결하기 위한 자료구조
blex.me
https://eusun0830.tistory.com/45?category=718944
[Python Algorithms] 트리(Tree) 1
트리 구조는 연결 리스트와 비슷하게 노드와 링크를 이용하지만 동작 구조는 매우 다르다. 트리는 그래프의 일종이며 서로 다른 두 노드를 잇는 링크가 하나뿐인 그래프를 트리라고 표현한다. 1
eusun0830.tistory.com
https://eusun0830.tistory.com/46?category=718944
[Python Algorithms] 트리(Tree) 2 : 순회 알고리즘
트리에서는 네 가지 순회 알고리즘을 가진다. 1) 전위 순회(Pre-Order Traverse) 2) 중위 순회(In-Order Traverse) 3) 후위 순회(Post-Order Traverse) 4) 단계 순위 순회(Level-Order Traverse) 1. 전위 순회 A..
eusun0830.tistory.com
https://lgphone.tistory.com/93?category=918750
14. 트리 순회 (Tree Traversal): 파이썬 자료구조와 알고리즘
순회 (Traversal) 란 트리 또는 그래프 같은 연결된 구조에서 객체 (노드) 를 방문하는 데 사용되는 알고리즘이다. 순회 문제는 모든 노드를 방문하는 방법을 찾거나 특정 노드만 방문하는 방법을
lgphone.tistory.com
'Computer Science' 카테고리의 다른 글
| [Computer Science] 자료구조 - Hash Table 해시 테이블 (0) | 2021.10.04 |
|---|---|
| [Computer Science] 자료구조 - 검색과 재귀(Searching and Recursion) (0) | 2021.10.04 |
| [Computer Science] 자료구조 - ADT(추상자료형) / linked-list/ Stack / Queue !!! (0) | 2021.10.04 |
| [Computer Science] 리팩토링과 최적화 -Refactoring, Data Optimization (0) | 2021.09.22 |
| [Computer Science] 예외처리(exception handling) - if ~else / try~except (0) | 2021.09.22 |


