[Computer Science] 자료구조 - Hash Table 해시 테이블

해싱 = 해시 맵 =해시 테이블

데이터 관리/유지 하는테이블 형태의 자료구조, 리소스를 이용하여 속도를 취함.

즉, key를 활용하여 value에 직접 접근이 가능한 구조로 정렬보다는 검색이 더 유용함.

 

구조

딕셔너리는 내부적으로 해시테이블 구조로 구현되여 있다. key-value형태로 저장

하나의 key는 하나의 value에 맵핑, key는 uniqueness를 보장함

# case 1 - 딕셔너리로 활용되는 해시테이블을 확인할 수 있다.

test_code = {2.5: 'A' ,'2.0': 'B', '1.0': 'C'}
print(test_code[2.5]) 
print(test_code['1.0'])
print(test_code['2.0'])

# case 2 - 리스트와 튜플을 활용해서 해시테이블을 확인한다.
# 데이터는 튜플로 저장된다.

test_code = [(2.5, 'A'), ('2.0', 'B'), ('1.0', 'C')]
 
def insert(item_list, key, value):
    item_list.append((key, value))
 
def search(item_list, key):
    for item in item_list:    # 데이터를 검색하려면 딕셔너리보다 오래 걸린다.(키,값 쌍이 없어서 개별 값으로 반복해서 검색하기 때문이다.)
        if item[0] == key:
            return item[1]      
    print('not matching')       
    
print(search(test_code, '2.0'))
print(search(test_code, 2.5))
search(test_code, 2.5)

 

 

해시 함수

규칙을 정하는 함수, 해시값을 부여하는 규칙을 부여함.

key 를 숫자(버킷, hashes, 해시값)로 바꿈.

입력값은 다양하고, 출력값은 정수형 숫자이다. 입력값이 같으면 동일한 출력값을 받는다. 

해시함수는 정 범위 안에 있는 숫자를 반환해야 한다.

• 하나의 해시함수가 입력 데이터별로 다른 숫자와 매핑된다면, 그것은 완벽한 해시함수이다.

기본해시함수

# 인코딩 예제
bytes_representation = "helo".encode()

for byte in bytes_representation:
    print(byte)
    
 # 정수값의 합 반환
bytes_representation = "hello".encode()

sum = 0
for byte in bytes_representation:
    sum += byte

print(sum)

# 해시함수를 만들고 활용해보자.
def my_hashing_func(str, list_size):
    bytes_representation = str.encode()

    print('str:',str)   # 검증코드
    print('str.encode():',str.encode())
    print('bytes_representation:',bytes_representation)
    
    sum = 0
    for byte in bytes_representation:
        sum += byte

    return sum % list_size

my_hashing_func("aqua", len(my_list))


# 먼저 5개의 빈 슬롯이 들어가는 리스트를 초기화시킨다.
my_list = [None] * 5

# 위의 my_hashing_func이라는 해시함수를 활용하여 아래처럼 값을 확인할 수 있다.
my_list = [None] * 5

my_list[my_hashing_func("aqua", len(my_list))] = "#00FFFF" # 리스트에 값을 저장

print(my_list[my_hashing_func("aqua", len(my_list))]) # 리스트에 있는 값을 출력

print(my_list)

 

시간 복잡도

Array처럼 리스트가 있지만 시간복잡도는 상수시간 O(1) (not always, but usually)

해시테이블의 사이즈에 관계없이 동일한 양의 계산을 다룬다. 

해시충돌로 인해 모든 bucket의 value를 찾아야 하는 반복문도 있다. 

만약 해시테이블이 하나의 요소를 갖고 있다면, 해시테이블 인덱스 갯수에 관계없이 프로그램 수행시간이 비슷하다.

• 검색 / 삽입 / 삭제 무엇을 하든지 해시함수는 키를 통해 저장된 값에 연관된 인덱스를 반환한다.(즉, 키와 인덱스가 매칭되야함)

 

해시 충돌collision

key가 들어갈 bucket(자리)이 없는 경우 발생한다. 

모든 값을 알고 있지 않으면 완벽한 해시함수 작성은 불가능 하다. 따라서 충돌이 적은 해시함수를 만드는 것이 해시테이블의 가장 중요한 목적이다. 

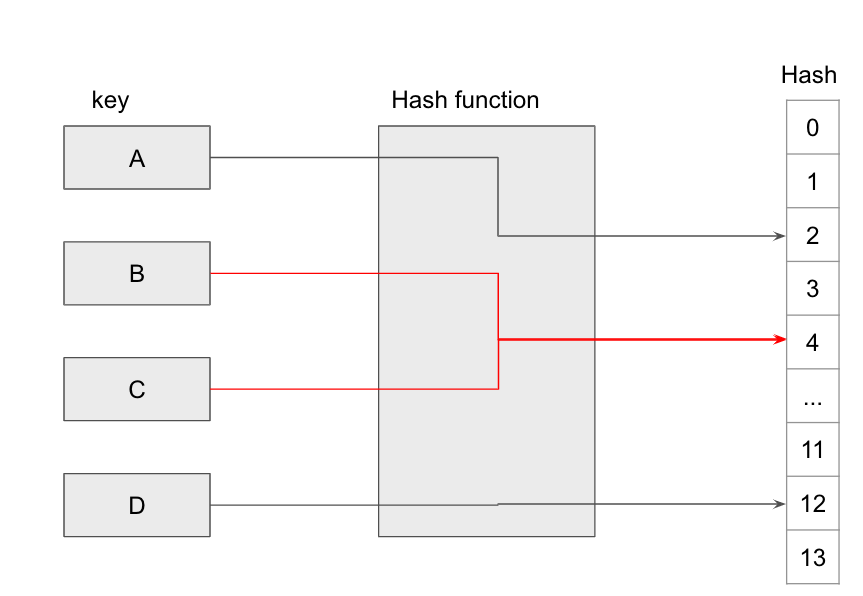
해시 충돌 해결

1. Chaining 체이닝
   Linked list를 사용, 해당 인덱스에 값이 있으면 값 뒤에 리스트 형식으로 값을 붙임.
   연결되는 entry에 제한을 두지 않고 체인형태로 연결한다. 
   

   

   
   
   • 해시 테이블에서 동일한 해시값에 대해 충돌이 일어나면, 그 위치에 있던 버킷에 키값을 뒤이어 연결한다.
   • 체이닝의 원리:
     1. 키의 해시값 계산
     2. 해시값을 이용해 리스트의 인덱스 추출
     3. 같은 해시값이 있다면 리스트로 연결.

   # 체이닝을 예시코드로 배워보자.
   # 아래와 같이 리스트안에 중첩되는 리스트를 만들어서 연결개념으로 해시테이블을 생성한다.
   
   chain_hash_table = [[] for _ in range(10)]  # 이번에는 10의 길이로 테스트를 진행한다.(0~9, 총 10개의 인덱스)
   print(chain_hash_table)
   '''[[], [], [], [], [], [], [], [], [], []]'''
   
   # 해시함수는 위와 동일하게 테스트할 수 있다.
   
   def chain_hash_func(key):
       return key % len(chain_hash_table)
   
   print(chain_hash_func(10)) #hash_key=0 
   print(chain_hash_func(20))  #hash_key=0 충돌 발생
   print(chain_hash_func(25))  #hash_key=5
   
   # append를 활용해서 키-값 쌍을 해시테이블에 삽입한다. 체이닝부분
   
   def chain_insert_func(chain_hash_table, key, value):
       hash_key = chain_hash_func(key)
       chain_hash_table[hash_key].extend(value)
       
   chain_insert_func(chain_hash_table, 10, 'A')
   print (chain_hash_table)
   '''[['A'], [], [], [], [], [], [], [], [], []]'''
   
   chain_insert_func(chain_hash_table, 25, 'B')    # 5번째 인덱스에 B가 삽입된다.
   print (chain_hash_table)
   '''[['A'], [], [], [], [], ['B'], [], [], [], []]'''
   
   # 아래 결과값과 같이 중첩되는 결과값이 있더라도 값이 대체(충돌)되는 것이 아니다.
   # 리스트 메소드 개념(list.append)이 활용되어 값을 이어 붙인다.('A' -> 'C')
   chain_insert_func(chain_hash_table, 20, 'C')    
   print (chain_hash_table)
   '''[['A', 'C'], [], [], [], [], ['B'], [], [], [], []]'''

2. open addressing(오픈 어드레싱):
   이미 만들어 놓은 버켓을 소모하자는 방식으로, 이미 만들어진 bucket을 찾아 value 넣음 - 추가 resizing bucket이 없으면 테이블을 더 크게 만들기도 한다.
   •  Linear Probing(선형 탐사): 고정폭으로 이동하여 빈공간을 찾음
   • Quadratic Probing: 제곱수로 이동하여 빈 공간을 찾음
   • Double Hashing: 또 다른 hash function을 사용하여 빈 공간을 찾음

 

Load Factor(로드 팩터)

해시 테이블에 저장된 항목 수(해시테이블에 입력된 키 갯수 )를 슬롯 수(해시 테이블 전체 인덱스 갯수 )로 나눈 값

로드팩터값을 통해 해시 테이블의 성능정도를 파악한다. 

위의 공식처럼 로드 팩터 비율에 따라 해시함수 재작성여부, 해시테이블 크기조정여부가 결정된다.

로드팩터를 낮추면 해시에 대한 성능이 올라간다. 

• 오픈어드레싱: 최대 로드 팩터는 1정도 나온다.
• 체이닝 : 로드 팩터는 오픈어드레싱보다 좋은 성능(로드팩터 <= 1)을 보일 수 있다.

 

좋은 해시 함수란?

해시 함수의 구현에 따라 해시의 성능이 결정된다. 

1. key-value 계산 과정이 쉬워야 한다. 

2. collision을 피할 수 있어야 한다. 

• 계산과정이 쉬운 경우
  • 체이닝(연결리스트)이 제대로 활용된다면 반복작업없이 해시의 검색 알고리즘을 활용하여 O(1)의 검색시간을 확보할 수 있을 것이다.
  • 해시값은 해시되는 데이터에 의해 완전히 결정된다.
  • 해시함수는 모든 입력 데이터를 사용해야 한다.
• 충돌을 피할 수 있는 경우
  • 해시함수는 가능한 해시값의 전체 집합에 데이터를 균일하게 배포한다.
  • 해시함수는 유사한 문자열에 대해 다른 해시값을 생성한다.

• 해시를 사용할 때 주의할 점
  • 키 데이터타입에 맞는 좋은 해시함수가 있는지 확인
  • 적절한 해시테이블 크기(배열크기)

 

 

 

---

ref. https://youtu.be/HraOg7W3VAM

https://youtu.be/xls6jEZNA7Y

ref. https://ahn3330.tistory.com/60?category=968900 

[자료구조] 7주차 - 해시 (Hash)

ref. https://www.youtube.com/watch?v=dKqv1mQotNU 

ref. http://wiki.hash.kr/index.php/%ED%95%B4%EC%8B%9C%ED%85%8C%EC%9D%B4%EB%B8%94

해시테이블 - 해시넷

ref. 

https://www.hackerearth.com/practice/data-structures/hash-tables/basics-of-hash-tables/tutorial/

Basics of Hash Tables Tutorials & Notes | Data Structures | HackerEarth