[Computer Science] 자료구조 다이나믹프로그래밍(Dynamic Programming) - 메모이제이션(Memoization)

다이나믹 프로그래밍 Dynamic Programming

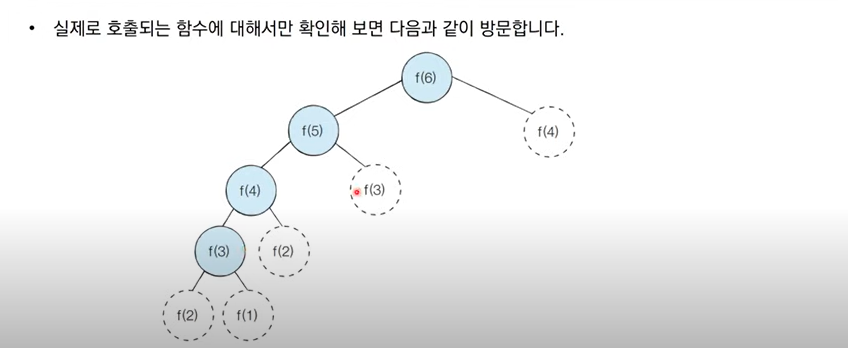
'문제의 일부분을 풀고 그 결과를 재활용하는 방법으로 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상 시키는 패러다임.
하나의 문제는 단 한번만 풀도록 하는 알고리즘
-탑다운과 보텀업으로 구성되어있다.

DP를 사용하게 되는 상황 : 이진 검색, 최단경로 알고리즘, 최적화 문제, 외판원 문제

!!! 분할 정복과의 차이점?

분할정복(Divide and Conquer)과 유사한 개념.

분할정복 기법은 동일한 문제를 다시 푼다는 단점이 있다.(=부분 문제, 서브문의 중복)

('정렬'과 같은 문제는 다시 풀게 되는 단점 없다, 그 예시로 퀵정렬과 병합 정렬이 있고 이 또한 매우 빠름)

 

다이나믹 프로그래밍 방식

다이나믹 프로그래밍의 구현은 일반적으로 두가지 방식으로 구성됨.

1. 탑다운(Top-Down) - 메모이제이션
   하향식, 구현과정에서 재귀 함수를 이용.
   큰 문제를 해결하기 위해 우선 작은 문제를 재귀적으로 호출하여 그 결과값을 메모이제이션을 이용하여 큰문제를 해결함. 
2. 보텀업(Bottom-Up) - 태뷸레이션
   다이나믹 프로그래밍의 전형적인 형태.
   상향식, 아래쪽에서 가장 작은 문제를 하나씩 해결해 나가면서 먼저 계산했던 값을 활용하여 그 다음 값을 계산하는 방식. 주로 반복문을 이용하며 해결.
   결과 저장용 리스트(다른 언어에서는 배열)는 DP테이블이라고 부름.

다이나믹프로그래밍 조건

DP는 분할정복에 아래의 개념이 추가된다. 

1. 최적 부분 구조(Optimal Substructure)
    메인문제를 서브문제로 나눌 수 있으며, 메인문제 해결방법을 서브문제에서 구하여 재사용 하는 구조로 메인문제를 해결 할 수 있다.
   • 정리 : DP는 최적 부분 구조로 구성된 중복된 서브문제를 분할정복으로 해결한다.
2. 중복되는 부분 문제(Overlapping Subproblem)
   메인문제와 서브문제를 같은 방법으로 반복하여 해결 할 수 있어야 한다. 

메모이제이션(Memoization)

다이나믹 프로그래밍을 구현하는 방법 중 하나. (탑타운 방식을 사용)
이미 계산한 결과는 배열(변수)에 저장함으로(메모리공간에 메모 = 캐싱 Caching) 나중에 동일한 계산을 해야 할때는 저장된 값을 단순히 반환 하기만 하면 되는 것. 

• 미리 계산한 값을 재사용하므로 프로그램 실행속도를 빠르게 해준다.
  • 메모이제이션은 동일한 입력을 가진 함수를 처음 호출할 때만 전체 호출 비용이 발생하도록 한다.
  • 메모이제이션은 함수의 시간 복잡도를 감소시키고, 공간 복잡도를 증가시킨다.
• 방법 : 반복되는 계산 결과를 특정 변수에 저장한다.
  • 아래 그림에서 'GETTING MEMO'를 통해 계산결과를 저장하고, 같은 함수에 대해서 'CALLING FUNCTION'을 활용하여 재사용한다.
    • 참고 : memoization은 컴퓨팅 작업을 위한 소프트웨어 기술이고, memorization은 과학분야에서 범용적으로 쓰일 수 있는 기법 또는 전략이라고 할 수 있다.

DP - 메모이제이션 코드 예제

1. 재귀함수 사용 

''' 메모이제이션 리스트로 저장 하기'''
memo = [0] * 100 # memoization 리스트 배열을 100개로 하여 초기화

# 피보나치 함수를 재귀 함수로 구현
def fibo(x):
    if x ==1 or x ==2:  # base case (1 혹은 2일때 1반환)
        return 1
    if memo[x] !=0 : # 이미 계산한 적 있는 문제라면 그대로 반환환
        return memo[x]
    # 아직 계산하지 않은 문제라면 점화식에 따라서 결과 memo[x]에 반환
    memo[x] = fibo(x-1) + fibo(x-2)
    return memo[x]

print (fibo(6))

# DP를 활용한 피보나치 수열
# 메모이제이션 dictionary형태로 저장

# 1) 재귀를 활용하여 주어진 문제해결을 위한 함수 먼저 생성
def dp_fib_cal(num, dp_memo):
    if num < 3:         # base case
        return 1        # 1과 2는 1로 반환환
    if num in dp_memo:  # dp_memo의 num 인자가 있으면 그 인덱스로 반환환
        return dp_memo[num]
    # dp_memo를 정의 해준다 문제 해결 과정 - 재귀 이용 피보나치 계산 
    dp_memo[num] =  dp_fib_cal(num - 1, dp_memo) + dp_fib_cal(num - 2, dp_memo) 
    # 계산된 값들을 dp_memo[num]에 저장해놓는다.
    
    return dp_memo[num]

# 2) 메모이제이션 개념을 위한 함수 생성
def dp(num):    
    dp_memo = {}    # 메모저장을 위한 변수생성
    return dp_fib_cal(num, dp_memo)

# 3) 함수를 호출하면서 문제를 발생시키는 곳이다.
print(dp(6))

'''
8
'''

• 딕셔너리에서 []는 키에 매핑되는 값을 할당하거나, 값 자체에 접근할 때 활용된다.
• key는 재귀되는 dp(num)함수의 파라미터값 num, value는 재귀되는 dp(num)함수에서 반환되는 값 이다.

2. 재귀 사용하지 않는 반복문 사용

# (1) 메모이제이션을 활용하지만 재귀는 활용하지 않는 DP
def fib_not_recur(n):
    arr = [j for j in range(n+1)]   # 컴프리헨션을 이용한 메모이제이션
    if n < 2:						# Base case
        return n
    for i in range(2, n+1):         # 피보나치 반복문 
        arr[i] = arr[i-1] + arr[i-2]
    return arr[n]

#(2) 함수를 호출하면서 문제를 발생시키는 곳이다.
print(fib_not_recur(6))

'''
8
'''

DP - Tabulation 코드 예시

'''보텀업 방식으로 피보나치 구현 - 타뷸레이션'''
# 타뷸레이션= DP table에 앞서 계산된 결과를 저장하여 사용한다
dp_table = [0]*100 # dp table 초기화

#첫번째 피보나치 수와 두번째 피보나치 수는 1인것을 dp table에 저장
dp_table[1] = 1
dp_table[2] = 1
n = 10

# 반복문으로 보텀업 다이나믹 프로그래밍
for i in range(3, n+1): # 3번째 부터 n+1번째까지의 범위 
    dp_table[i] = dp_table[i-1]+dp_table[i-2]

print(dp_table[n])

 

 

 

ref. https://www.youtube.com/watch?v=5Lu34WIx2Us 

https://blog.naver.com/ndb796/221233570962

20. 다이나믹 프로그래밍(Dynamic Programming)

https://namu.wiki/w/%EB%8F%99%EC%A0%81%20%EA%B3%84%ED%9A%8D%EB%B2%95?from=%EB%8F%99%EC%A0%81%EA%B3%84%ED%9A%8D%EB%B2%95